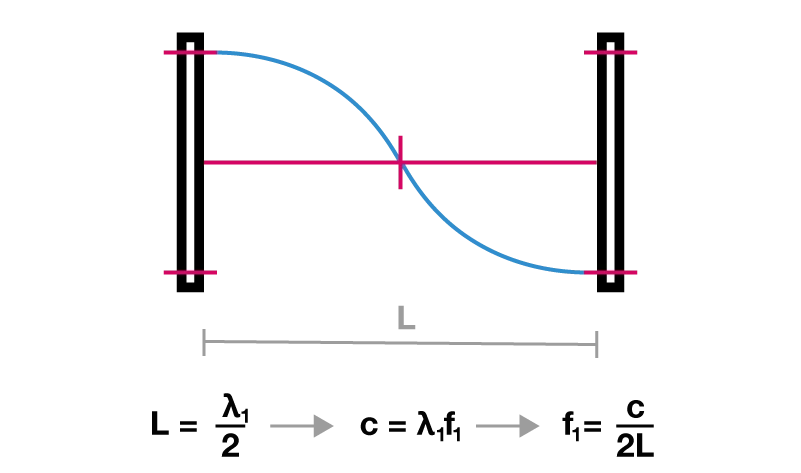
Primo modo naturale di una coppia di pareti riflettenti
Per iniziare ad affrontare l'approccio dell'analisi ondulatoria o modale, facciamo un richiamo ai modi naturali di un sistema risonante. Partiamo dallo studio dei modi naturali di una coppia di pareti parallele perfettamente riflettenti. Queste pareti determinano dei vincoli per il campo acustico, quindi impongono sostanziaomente che se il campo acustico è espresso attraverso la grandezza della pressione acustica, in corrisondenza delle pareti ci siano due ventri (due massimi della espressione). In questo modo, ponendo un nodo al centro del sistema, posso disegnare il profilo di pressione del modo naturale più grave del sistema stesso.

Primo modo naturale di una coppia di pareti riflettenti
Aggiungendo un altro nodo otteniamo il profilo di pressione del secondo modo naturale del sistema:
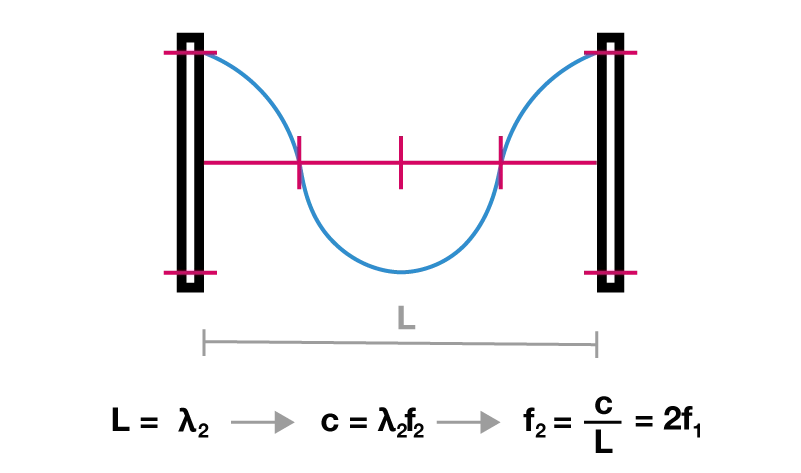
Secondo modo naturale di una coppia di pareti riflettenti
Andando così avanti, otteniamo una famiglia di modi naturali, per i quali la frequenza associata ad ognuno è uguale a fn = n * f1. Analizzando questo metodo deduciamo che le frequenze di un ipotetico suono che sono in relazione alla famiglia armonica del sistema durano più a lungo nel tempo, tutte le frequenze che invece non ne fanno parte si estinguono in minor tempo in quanto non soddisfano i vincoli delle due pareti. Il risultato della sovrapposizione di tutte queste onde stazionarie armoniche, considerando il teorema di Fourier, sarà un segnale periodioco, cioè armonico e cioè dotato di intonazione (pitch). Chiamiamo questo risultato di sovrapposizioni risposta in frequenza h(t).