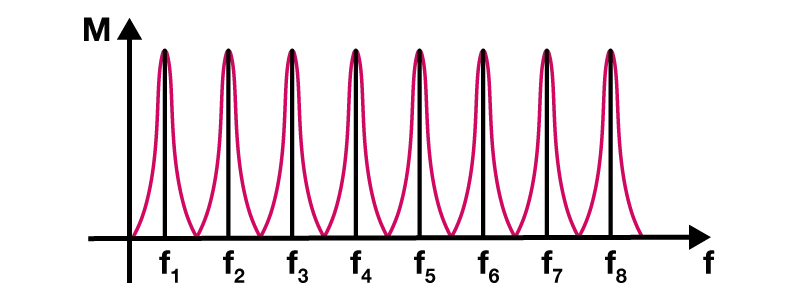
Grafico risposta in frequenza
Nel grafico della risposta in frequenza possiamo notare dei picchi di risonanza in prossimità delle frequenze appartenenti alla serie armonica.

Grafico risposta in frequenza
Questo sistema risulta valido quando il nostro spazio somiglia ad esso, possiamo dunque applicarlo in gallerie, grandi garage (considerando soffitto e pavimento in quanto le pareti sono molto lontane). Qualsiasi sistema lineare tempo invariante si può esprimere attraverso la funzione della risposta all'impulso. La risposta all'impulso è l'uscita del sistema quando gli diamo in ingresso una funzione matematica particolare che si chiama impulso di dirac. L'impulso per definizione è una funzione matematica che rispetto all'operazione di convoluzione è come se fosse neutra, quindi è come se valesse 1. Quando faccio una convoluzione tra un impulso di dirac e la risposta all'impulso ottengo la risposta all'impulso: i(t) * h(t) = h(t). La risposta all'impulso in sostanza è la funzione che mi permette di sondare tutte le proprietà di quel sistema e di ritrovarmele in uscita. Bisogna ricordare che nel caso della risposta in frequenza di un ambiente, essa vale solo per quella specifica disposizione sorgente-emettitore usata in fase di analisi. Cambiando questa disposizione, otterrò sempre risposte all'impulso differenti.
Data la risposta all'impulso, attraverso la trasformata di Laplace, posso derivare la funzione di trasferimento del filtro H(s).
Questa (s) è una variabile complessa definita nel dominio di Laplace. Dentro di sè questa funzione di trasferimento ha tutte le informazioni che ha la risposta all'impulso, soltanto che viene vista in un dominio diverso, un dominio trasformato.
Nel momento in cui calcoliamo questa funzione per una direzone partiolare di questa variabile, cioè quando s = jω, otteniamo la risposta in frequenza H(jω).
La risposta in frequenza ci permette di visualizzare sia lo spettro del modulo sia lo spettro della fase.
Ricavando la risposta in frequenza, in realtà taglio fuori tutta quella parte della funzione di trasferimento che riguarda il tempo, ovvero il transitorio di quel sistema.
Vogliamo dunque sottolineare che la risposta in frequenza ci restituisce il comportamento del filtro in condizioni stazionarie, cioè quando è passato un po di tempo e il sistema si è assestato.
Ricapitolando, l'approccio allo studio di un ambiente attraverso l'analisi dei suoi modi naturali è vero e risulta valido per le condizioni di stazionarietà di quel sistema, cioè quando è passato un tempo sufficiente affinchè la famiglia di onde stazionarie si è stabilita all'interno tra le due pareti.
Nella risposta all'impulso ho comunque tutte le informazioni del sistema, ma nel momento in cui ricavo la risposta in frequenza vedo solo quelle relative alla parte stazionaria del sistema.
Il profilo di filtraggio della risposta in frequenza viene chiamato comb in quanto assomiglia di fatto ad un pettine.