fig. 3 - \(s(1) = \sqrt 1\)
Consideriamo la funzione non lineare \(s(x) = \sqrt x\).

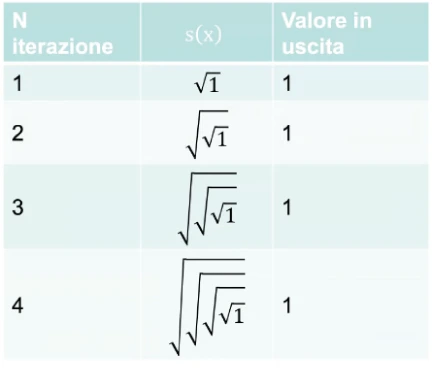
fig. 3 - \(s(1) = \sqrt 1\)
Qualsiasi sia l’iterazione, la risposta presenta sempre il valore 1. Il valore 1 è detto punto fisso
dell’iterazione. Vediamo cosa succede se ci spostiamo di poco.
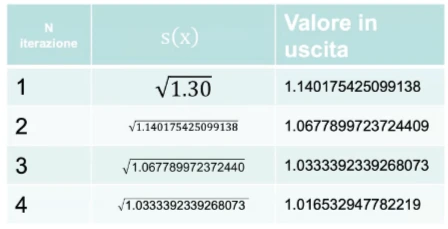
fig. 4 - \(s(1.30) = \sqrt 1.30\)
Notiamo che al crescere dell’iterazione, la risposta tende al valore 1, cioè al punto fisso.
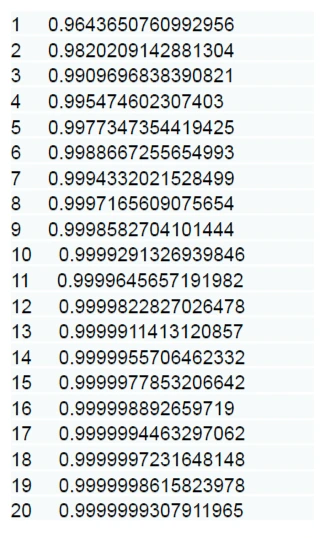
fig. 5 - \(s(0.93) = \sqrt 0.93\)
Al crescere dell’iterazione, anche in questo caso la risposta tende al valore 1, cioè al punto fisso.

fig. 6 - \(s(0.2) = \sqrt 0.2\)
Anche con \(x = 0.2\) si arriva rapidamente al punto fisso \(x = 1\).
L’insieme dei valori prodotti dalle successive iterazioni del valore di partenze viene detta orbita del punto.
Di seguito un programma in Python che stampa i valori dell’orbita della iterata della funzione \(s(x) = \sqrt x\).
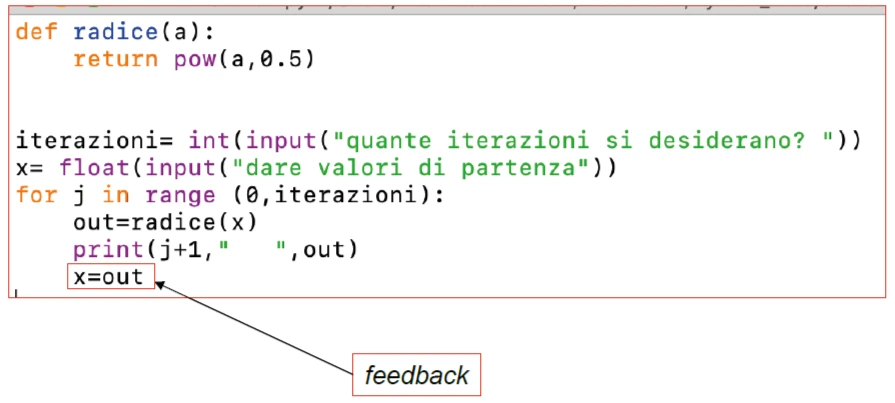
fig. 7 - Punto fisso in Python