fig. 8
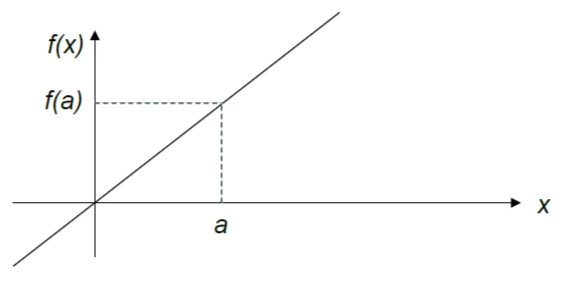
Un modo differente per verificare i punti fissi è attraverso il grafico. Consideriamo infatti la funzione \(y(x) = x\) che associa al punto dell’immagine \(y\) il valore attuale del punto sul dominio.

fig. 8
Consideriamo ora una funzione non lineare che insiste sullo stesso grafico. Preso un punto iniziale sull’asse delle ascisse, prendiamo il valore corrispondente sull’asse delle ordinate e proiettiamo il valore ricavato sulla retta \(y = x\) per poter ricavare il nuovo punto di partenza sull’asse delle ascisse.
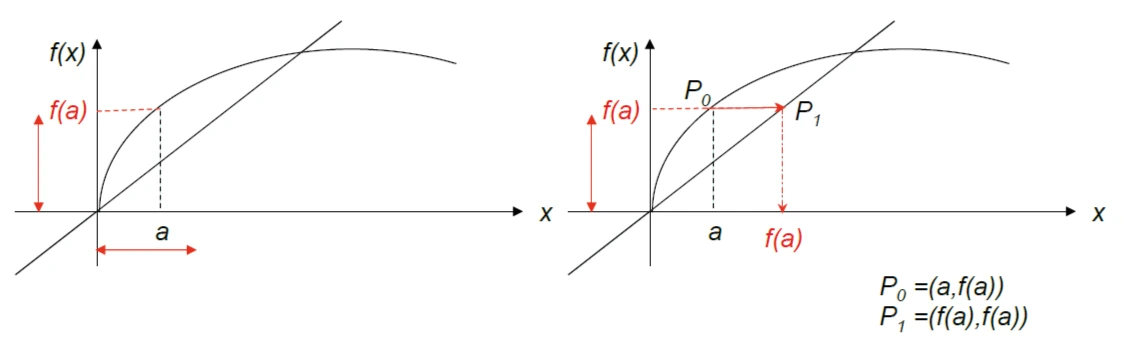
fig. 9
Procediamo in modo analogo per determinare il nuovo punto f(f(a)).
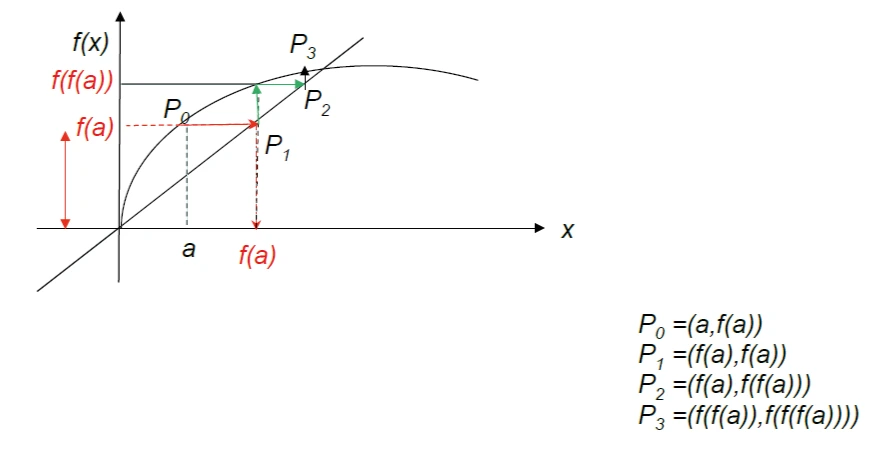
fig. 10
La figura seguente illustra la reiterata \(s(x) = \sqrt x\) del punto \(x < 1\); si vede chiaramente che l’orbita tende al punto fisso 1.
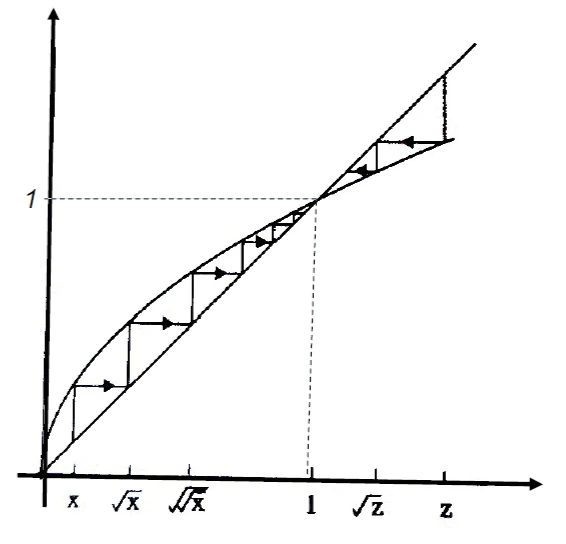
fig. 11
Il coseno ha un punto di attrazione 0.73908. Mentre per le funzioni dispari vediamo che abbiamo due punti di attrazione. I punti della \(x^2\) vengono detti punti fissi repulsori.
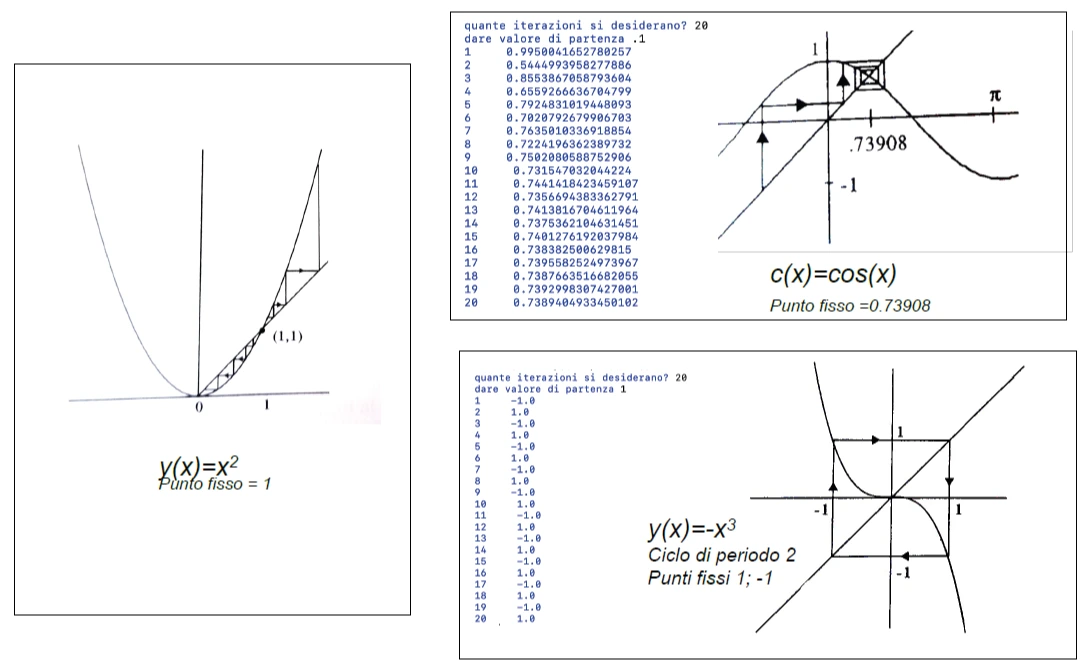
fig. 12