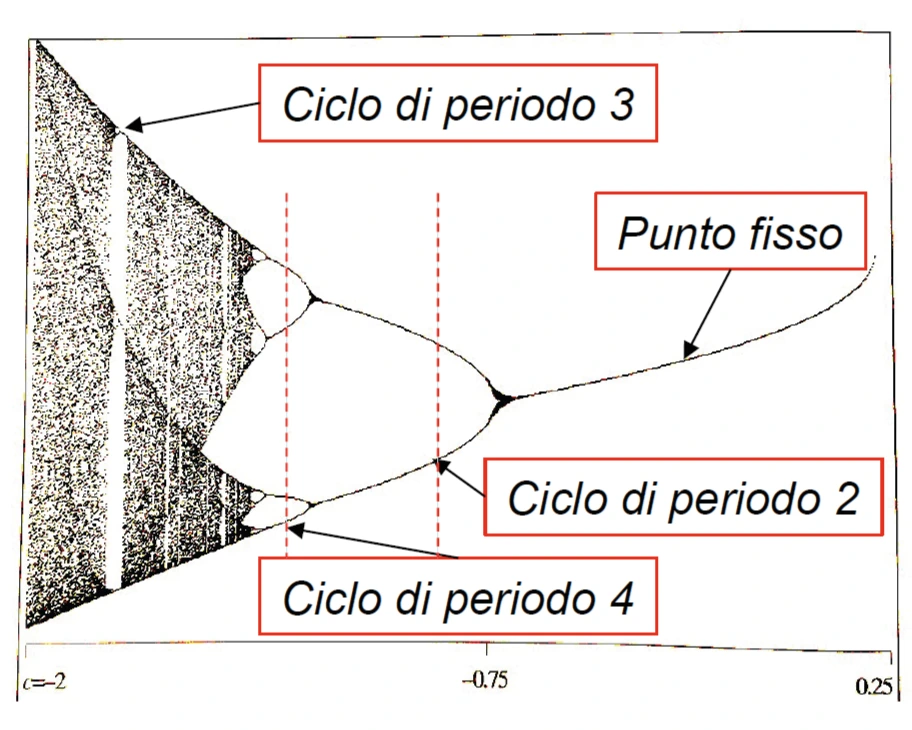
fig. 18
Può essere utile visualizzare il comportamento dell’equazione logistica o di una equazione quadratica, al variare del parametro \(c\), tenendo costante il punto di partenza. Il grafico corrispondente ha sulle ascisse il valore di \(c\) e sulle ordinate i valori dell’orbita, in base al valore di partenza fissato. Consideriamo la funzione \(F(x) = x^2 + c\) e reiteriamola nel punto iniziale \(x = 0\) esplorando i valori di \(c\) da -2 a 0.25. Si osserva che per \(-0.75 < c < 0.25\) è presente un solo punto fisso, quindi lo 0 è stato “attirato” da un unico punto fisso. In prossimità di -0.75 appare una prima biforcazione, con un ciclo di periodo 2.

fig. 18
Se si effettua un ingrandimento, cioè si raffina lo step di \(c\) e si esplorano i valori per di \(c\) da -1.65 a -0.75 otteniamo il seguente diagramma delle orbite
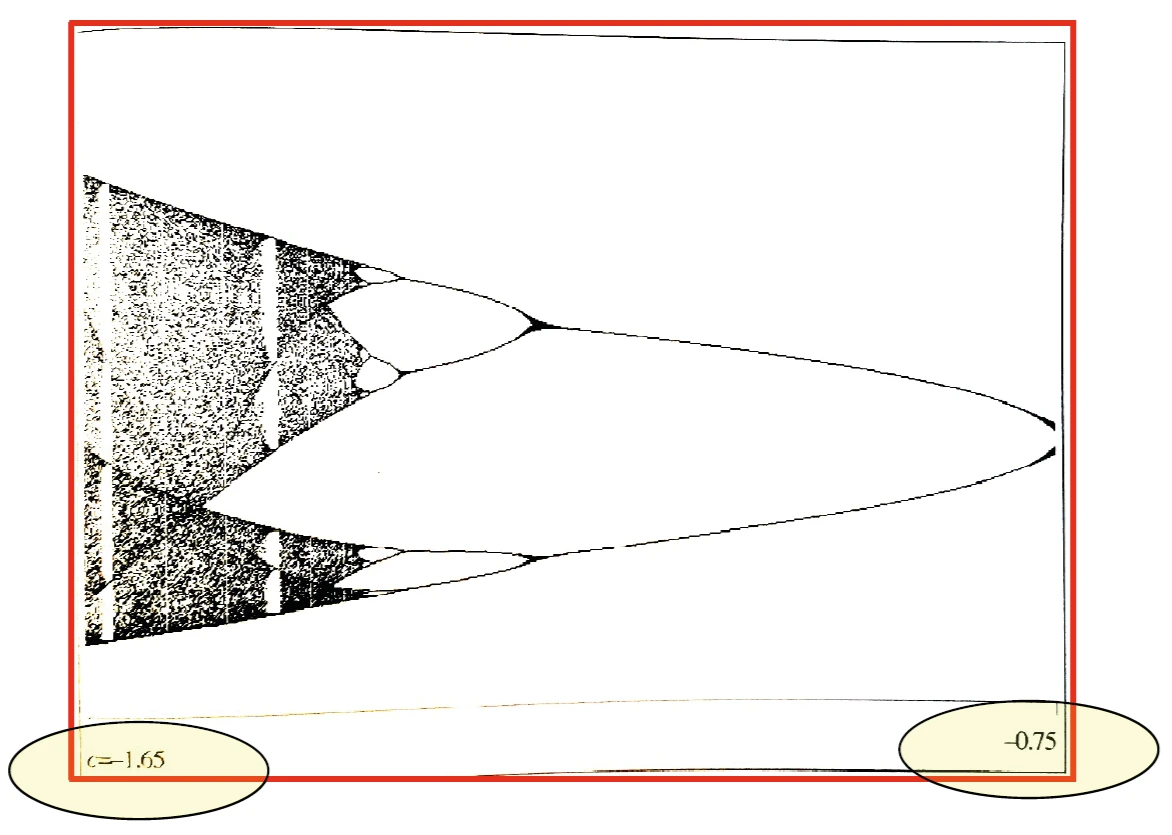
fig. 19
Il diagramma dell’ingrandimento è “simile” all’originale.
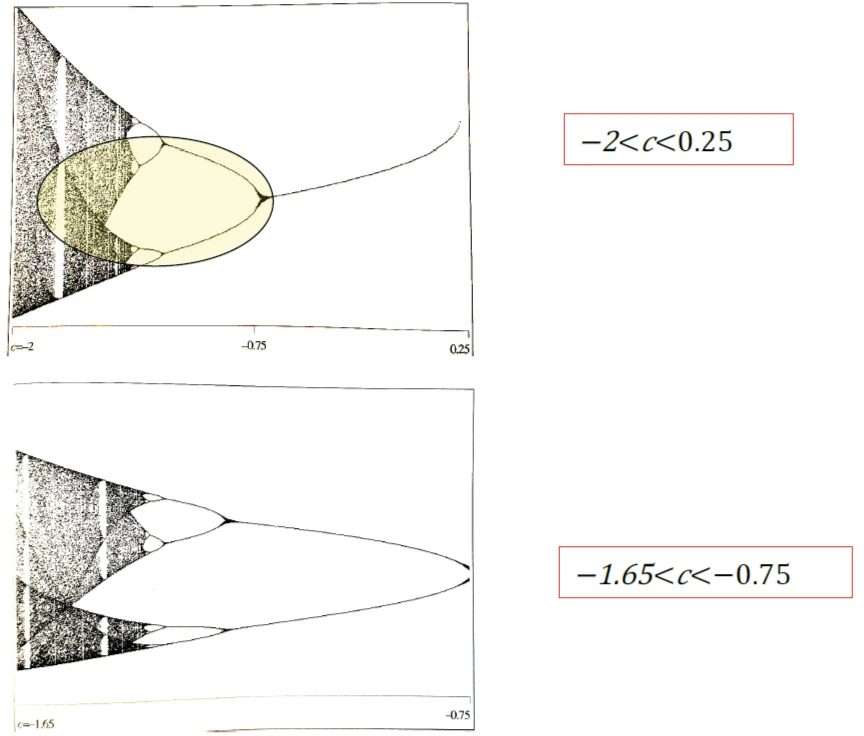
fig. 20
The logistic map connects fluid convection, neuron firing, the Mandelbrot set and so much more.
Animations, coding, interactives in this video by Jonny Hyman.
Try the code yourself