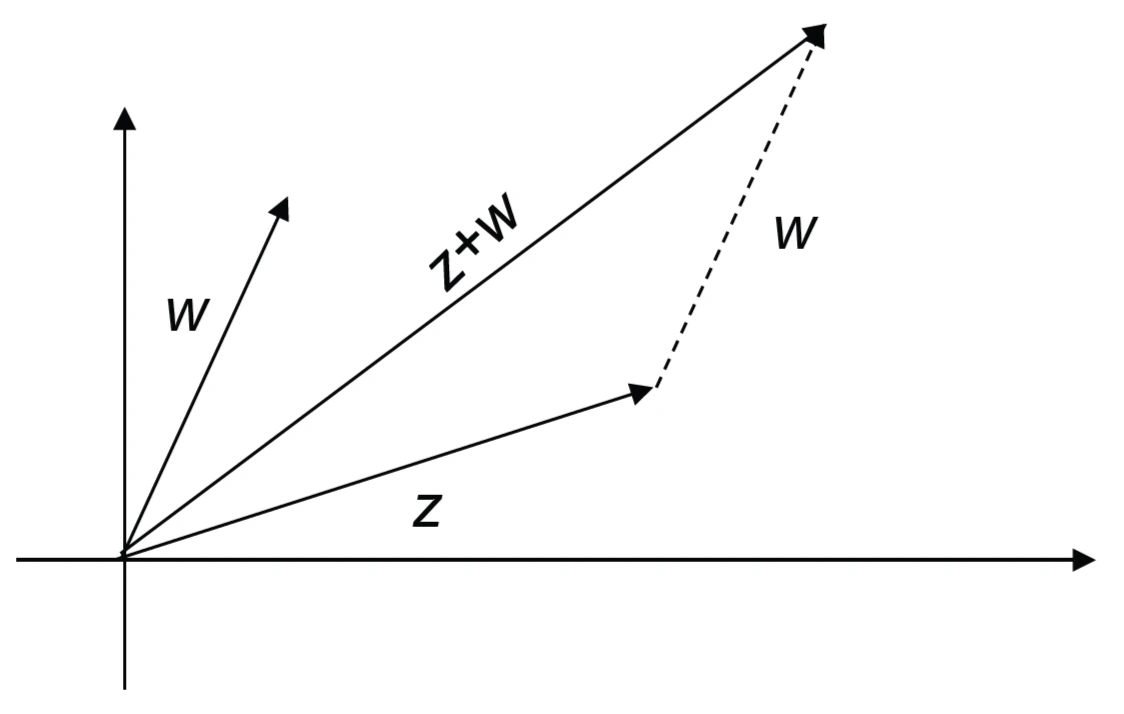
fig. 21 - Rappresentazione geometrica di una somma di due numeri complessi
Ricordiamo che un numero complesso è caratterizzato da un modulo e una fase e può essere rappresentato in forma cartesiana \(z = x + jy\) oppure polare \(z = \rho ( \cos (\varphi) + j\sin (\varphi) ) = \rho \cdot e^{j\alpha}\).
Il prodotto tra due numeri complessi può essere risolto algebricamente attraverso la rappresentazione cartesiana oppure attraverso la rappresentazione polare.
\(z_1 = x_1 + jy_1 = \rho_1 \cdot e^{j\varphi}\); \(z_2 = x_2 + jy_2 = \rho_2 \cdot e^{j\alpha}\);
\(z_1 \cdot z_2 = (x_1 + jy_1) \cdot (x_2 + jy_2) = (x_1 \cdot x_2 - y_1 \cdot y_2) + j(x_1 \cdot y_2 + y_1 \cdot x_2)\);
\(z_1 \cdot z_2 = \rho_1 \cdot e^{j\varphi} \cdot \rho_2 \cdot e^{j\alpha} = \rho_1 \cdot \rho_2 \cdot e^{j(\varphi + \alpha)}\)
\(z^2 = \rho^2 \cdot e^{j2\varphi}\); l'elevazione al quadrato implica una rotazione del modulo del vettore \(z\) sul piano complesso. Fare la somma dei due vettori vuol dire applicare la regola del parallelogramma.

fig. 21 - Rappresentazione geometrica di una somma di due numeri complessi
È interessante notare che facendo il modulo di \(z + w\) avremo un valore piú piccolo rispetto al modulo di \(z\) più il modulo di \(w\).
Disuguaglianza triangolare (Disuguaglianza di Cauchy-Schwartz): \(|z + w| \leq |z| + |w|\)
Consideriamo l’iterazione della funzione quadratica \(T(z) = z^2 = (x + jy)^2 = (x^2 - y^2) + j(2xy)\)
Proviamo ad iterare la funzione complessa su un punto iniziale \(\in |x| \leq 2 ; |y| \leq 2\)
Il risultato è che tutti i punti \(z\) il cui modulo è \(< 1\) convergono al punto fisso 0, mentre se \(|x + jy|> 1\) i punti tendano all’infinito.
Cosa succede quando \(|x + jy| = 1\)? Questi punti ∈ alla circonferenza unitaria nel piano di Gauss.
Tutti questi punti saranno quelli che appartengono alla circonferenza di raggio 1.
L’insieme di questi punti è detto insieme di Julia.
Si può dimostrare che l'orbita di un punto \(\in\) all'insieme di Julia, rimane per sempre nell'insieme di Julia.