
fig. 25
E’ generato da una successione infinita di “rimozioni”. Si inizia con un triangolo equilatero pieno e dal suo interno si rimuove il triangolo i cui vertici sono a \(L / 2\) rispetto alle lunghezze dei lati del triangolo di partenza.

fig. 25
Successivamente si ripete lo stesso procedimento ai tre triangoli che si generano.

fig. 26
E così via, con la successiva rimozione.

fig. 27
E’ una figura autosimilare? Basta prendere una porzione e confrontarla con la figura originale. L’area del triangolo di Sierpinski è pari a 0 ma il perimetro è finito.

fig. 28
Implementazione Sierpinski:
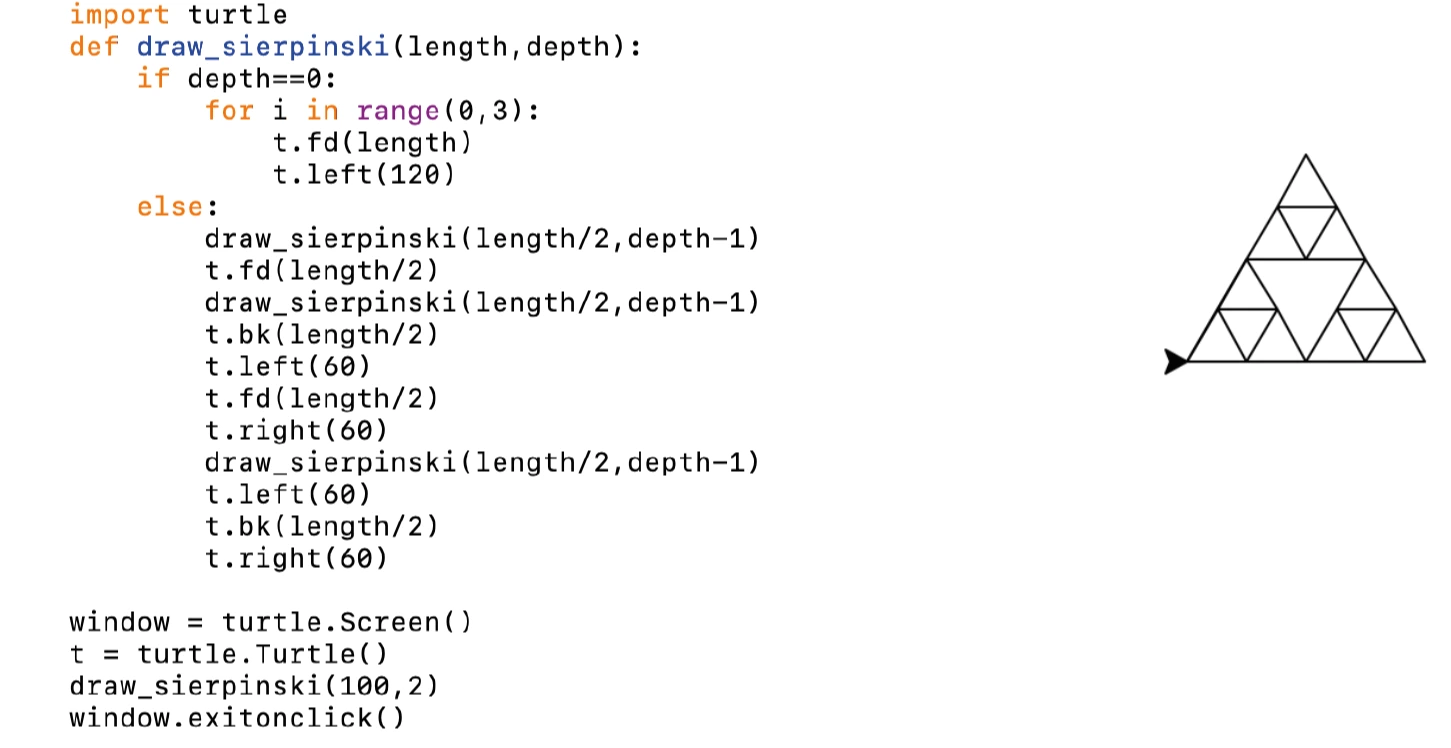
fig. 29