fig. 38
La distribuzione descrive fenomeni per cui la variabile casuale \(x\) assume valori interi maggiori o uguali a zero.
La funzione non ha limite superiore e la distribuzione è controllata dal parametro \(\lambda\).
La probabilità di avere l’intero \(k\) è data da: \(p {x = k} = e^{-\lambda} \frac{\lambda^k}{k!} \; x > 0\)
Il valor medio della distribuzione è \(\lambda\).
\(\lambda\) indica il numero di eventi che mediamente in successione e in un dato intervallo di tempo si verificano.
\(k\) indica il numero di eventi per un dato intervallo di tempo del quale si vuole conoscere la probabilità che si verifichino.
\(\lambda\) è uguale al numero aspettato delle occorrenze che accadono durante un intervallo di tempo dato.
Ad esempio se l’evento o il gruppo di eventi accade ogni 5 minuti, per conoscere quanti eventi accadono in un intervallo di 20 minuti, basta:

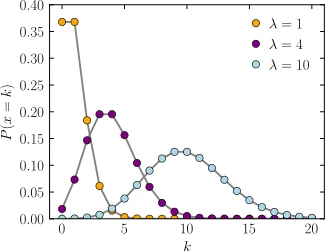
fig. 38
Nell'immagine fig.38 consideriamo \(\lambda = 4\);
supponiamo inoltre che in 5 minuti accadono 10 eventi;
se desideriamo sapere la probabilità di avere \(k \cdot 10\) eventi in 20 minuti basta osservare il grafico sulla sinistra.
(\(k\) è indicato in ascisse e rappresenta il gruppo di eventi o l’evento).
Avrò quindi la probabilità del 20% (0.2) di avere \(3 \cdot 10 = 30\) eventi o \(4 \cdot 10 = 40\) eventi in 20 minuti.
Ci sarà invece la probabilità del 7% (0.07) di avere \(1 \cdot 10\) eventi.
La distribuzione di Poisson è legata al processo di Poisson.
Si applica a vari fenomeni di natura discreta (ovvero quelli che possono accadere 0, 1, 2, 3,… volte durante un periodo di tempo o in una data area) ma con il vincolo che la probabilità rimanga costante nel tempo (o nello spazio in caso di
area).
Esempi di eventi che seguono il modello di Poisson sono:
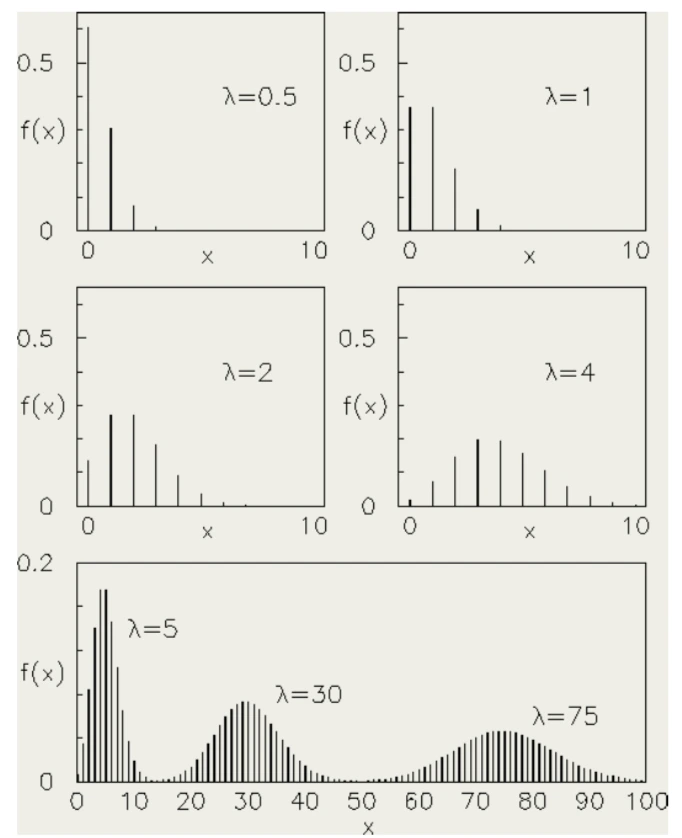
fig. 39
La distribuzione è detta anche degli eventi rari. E’ stata usata da Xenakis per la distribuzione di altezze e durate nei suoi lavori. Per Xenakis tale distribuzione descrive un andamento di molte “individualità” che però marciano verso un obiettivo, come succede per la folla durante una manifestazione. Se un individuo intona uno slogan, questo può morire subito (se non viene recepito da un numero sufficiente di individui), oppure crescere fino a diventare collettivo.