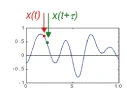
fig.41
Se il segnale varia in modo monotono, (lentamente nel tempo) allora x(t- τ) è simile a x(t) quindi il prodotto sarà diverso da zero (e positivo) e l’indice di correlazione sarà maggiore di zero.
L’autocorrelazione Rx(τ) fornisce una misura di quanto un segnale si assomigli, si correli, abbia in
qualche modo proprietà comuni con se stesso ritardato di un tempo t. In altre parole
l’autocorrelazione segnala se una sequenza o un segnale contengono dei pattern che si ripetono.
L’autocorrelazione viene calcolata come il valor medio del prodotto di un valore xk della variabile
aleatoria con tutti i valori assunti dalla variabile aleatoria stessa. Se i valori non coincidono allora non ci
sarà autocorrelazione poiché il valor medio del prodotto tenderà a zero.

fig.41
Se il segnale varia in modo monotono, (lentamente nel tempo) allora x(t- τ) è simile a x(t) quindi il prodotto sarà diverso da zero (e positivo) e l’indice di correlazione sarà maggiore di zero.
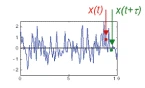
fig.42
Se invece ho un processo con rapide variazioni, x(t- τ) è diverso da x(t) quindi il loro prodotto darà un segno casuale, e la somma di tutti i prodotti sarà prossima allo zero.
L’autocorrelazione ha molte applicazioni: ex riesce a ricavare un segnale nascosto dal rumore
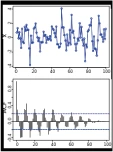
fig.43
Il segnale casuale di 100 campioni contiene anche una sinusoide.
La correlazione evidenzia la sinusoide nascosta (correlogramma).
E’ possibile intendere l’autocorrelazione come un indice di “memoria” di un processo casuale. Se gli
stati immediatamente precedenti allo stato attuale influenzano tale stato (cioè il valore attuale è legato
ai valori precedenti per somiglianza numerica) allora l’autocorrelazione avrà un valore
significativamente diverso da zero e saremo in presenza di processi con memoria.
Mentre la densità di probabilità contiene l'informazione relativa alle variazioni d'ampiezza del
processo, (cioè relativa ai valori che assume la variabile casuale X), l'autocorrelazione contiene
l'informazione relativa alle variazioni della variabile casuale X sull'asse dei tempi (legata quindi
alla frequenza di ripetizione del fenomeno).
La trasformata inversa di uno spettro di densità rappresenta l'autocorrelazione del segnale.