fig. 48
Negli esempi precedenti abbiamo descritto il Random walk, che implica che
lo stato successivo raggiunto dal sistema sia adiacente (gradino successivo o
precedente) rispetto a quello attuale.
Una molecola di gas si muove nello spazio istante per istante in questo
modo, non potendo saltare da un punto all’altro dello spazio.
Per implementare un random walk tridimensionale saranno necessarie 3 matrici
di probabilità rispettivamente per le tre dimensioni spaziali x,y,z. La traiettoria
della particella sarà f(x,y,z,t)

fig. 48
Possiamo considerare un sistema in modo più generale, con la transizione ad uno stato successivo, non adiacente allo stato precedente. Questo aspetto è particolarmente interessante quando si tratta di articolare nel tempo parametri musicali come le altezze, durate, pan, ecc.
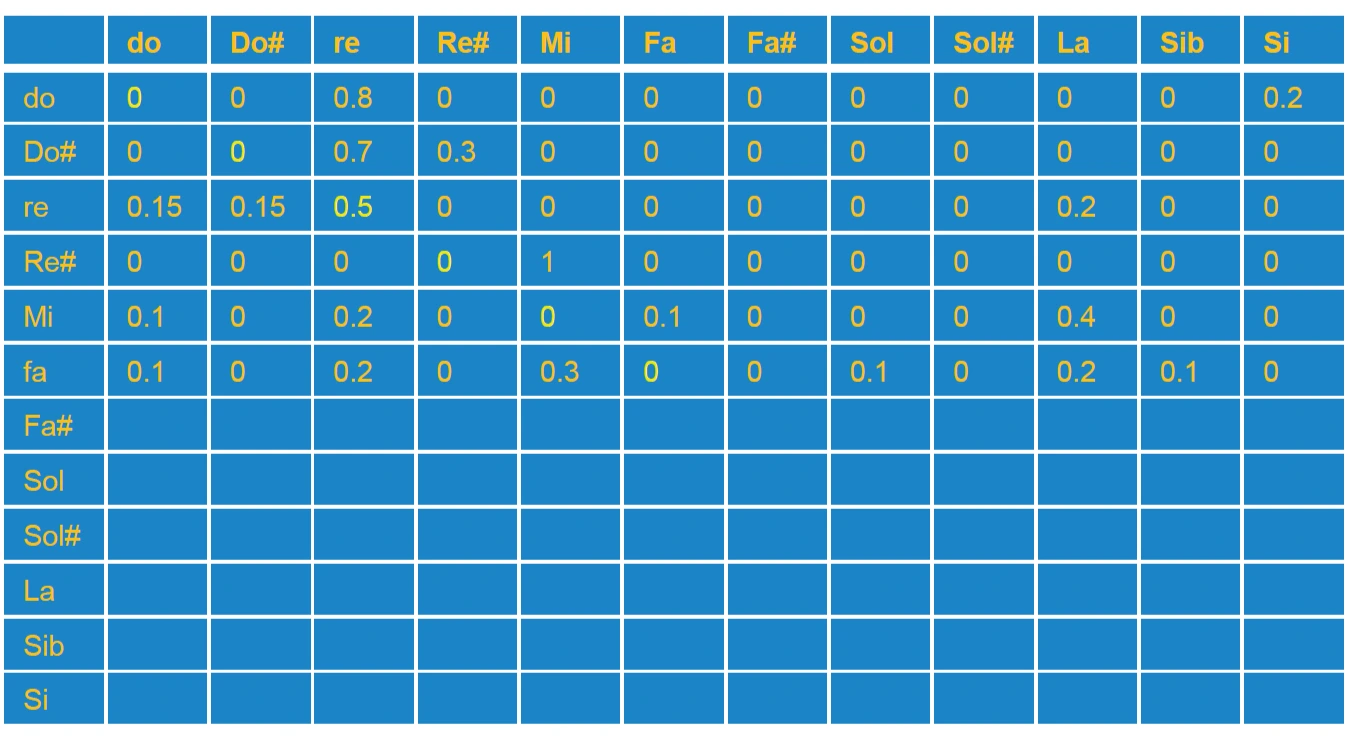
fig. 49
La matrice in esempio (da completare) indica la probabilità di avere una nuova altezza, a partire da un’altezza fissata.
Come si può osservare la diagonale principale ha tutti 0 ad eccezione del re (0.5) che subisce un peso maggiore (polarizzazione).
Per ricavare una matrice markoviana da un flusso di dati in ingresso, bisogna verificare le occorrenze (numero di volte in cui si presenta un evento frequenza]) e costruire successivamente la matrice delle probabilità dividendo in numero
di occorrenze per il numero totale di eventi.
Da sequenze MIDI si possono estrarre le occorrenze e la matrice di probabilità ed in tal caso è possibile iniziare ad effettuare una analisi delle occorrenze (altezze e durate) al fine di una ri-produzione stilistica.