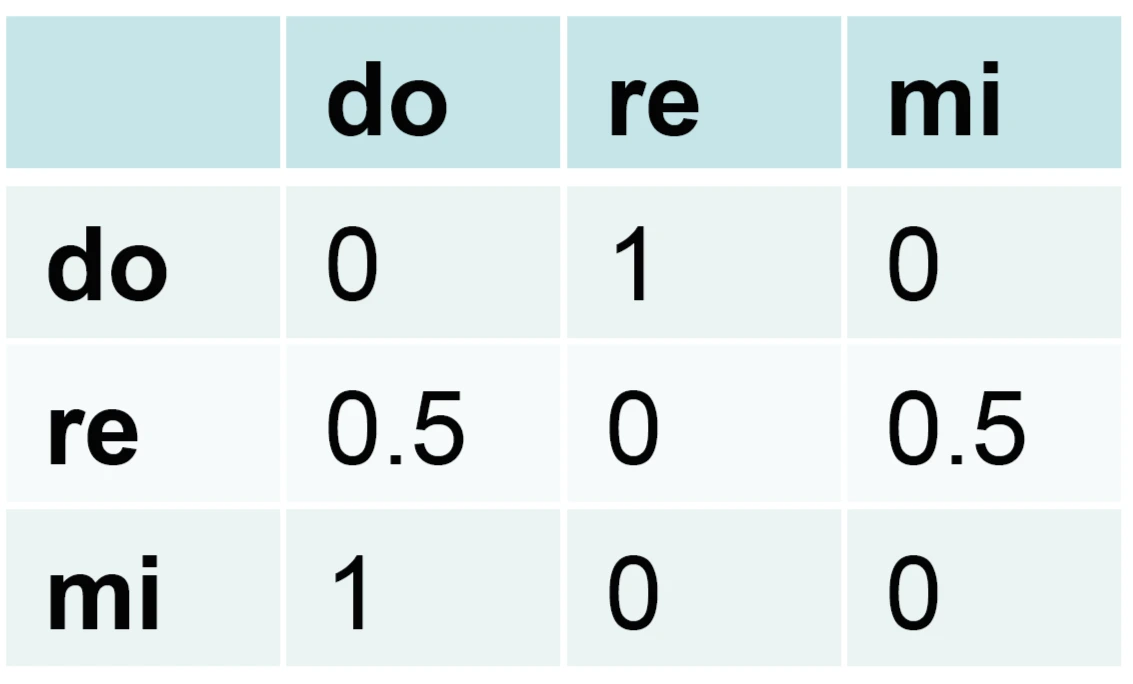
fig. 54
Matrice di transizione del 1 ordine
Per ottenere una matrice di Markov del 2 ordine bisogna verificare le occorrenze di ogni
nuovo stato a partire dall’essersi verificata una coppia di stati.
Consideriamo 3 altezze: do, re, mi e una matrice di transizione del primo ordine:

fig. 54
Matrice di transizione del 1 ordine
Consideriamo ora la probabilità che si verifichi uno dei tre eventi (do,re,mi) dopo che si sia verificata una coppia di eventi.
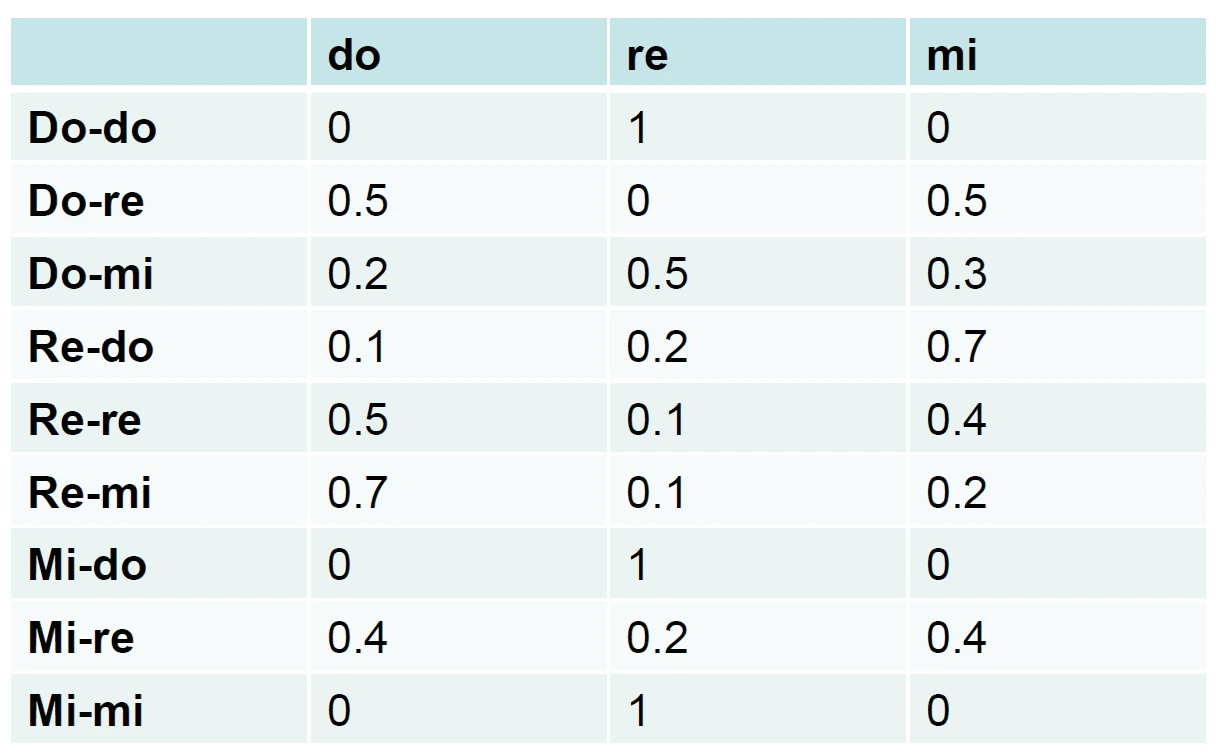
fig. 55
Matrice di transizione del 2 ordine
Supponiamo ora di partire dalla coppia Re-mi: l’algoritmo individua la prima
colonna cioè la nota do. A questo punto la vecchia coppia Re-mi viene sostituita
con la coppia mi-do.
Ad esempio:
Re-mi → do
Mi-do → re
Do-re → mi
Mi-re → do
ecc
E’ come considerando il Re-mi iniziale, spostassi il Re sulla sinistra, non considerandolo più e considerassi la nuova coppia MI-DO.
L’algoritmo proposto intende fare la stessa operazione, utilizzando la codifica MIDI delle
altezze.
Spostare un numero verso sinistra di una posizione è analogo a moltiplicare quel numero
per il sistema posizionale scelto: ad esempio se il numero 123 viene spostato verso
sinistra di una posizione diventa 1230 ed è analogo ad avere moltiplicato 123 per 10.
Spostare di due posizioni implica moltiplicare per 100.
In Max l’oggetto << sposta il numero delle posizioni indicate dalla cifra che segue << , in base ad un sistema posizionale basato sul 2.
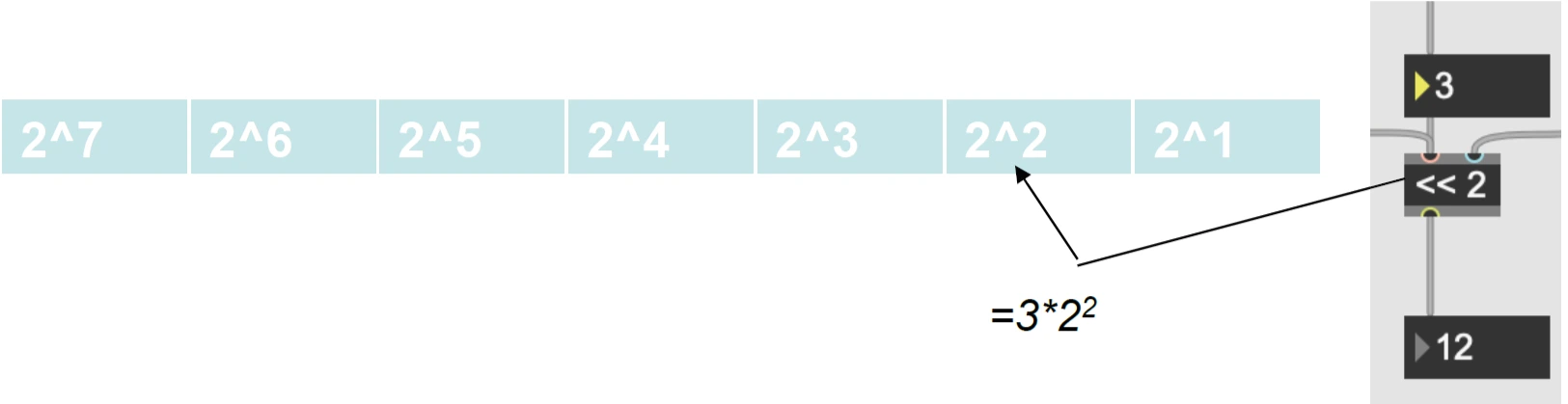
fig. 56
L’oggetto bucket ricorda il dato in ingresso all’oggetto e lo restituisce in uscita
all’arrivo del dato successivo.
L’algoritmo prende due note consecutive MIDI, la prima delle quali viene shiftata di 7
posizioni (7 bit) e aggiunge a tale numero generato la nota MIDI attuale, generando un
unico numero.

fig. 57
L’oggetto anal riporta quante occorrenze sono state effettuate di una coppia di
numeri in ingresso.
Nell’algoritmo considerato, vengono contate le occorrenze di coppie di numeri che
contengono già una coppia per ogni numero, realizzata con lo shift.
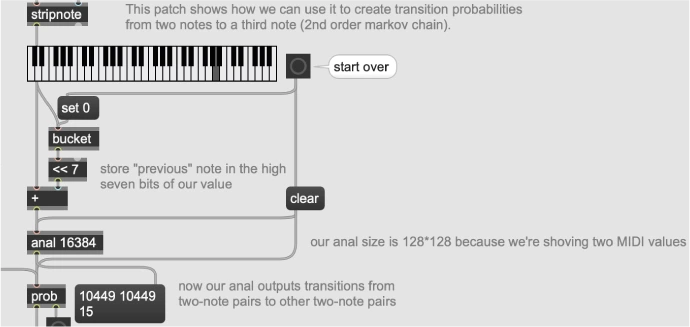
fig. 58
L’oggetto prob ricava una matrice di probabilità a partire dalla occorrenze in ingresso.
L’oggetto % 128 estrae il resto della divisione per 128 (7 bit) riportando il numero ad
un valore compreso tra 0 e 127.
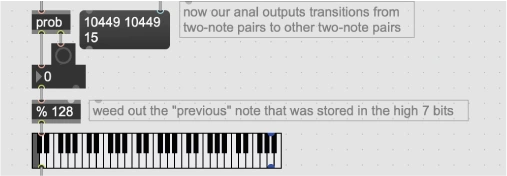
fig. 59
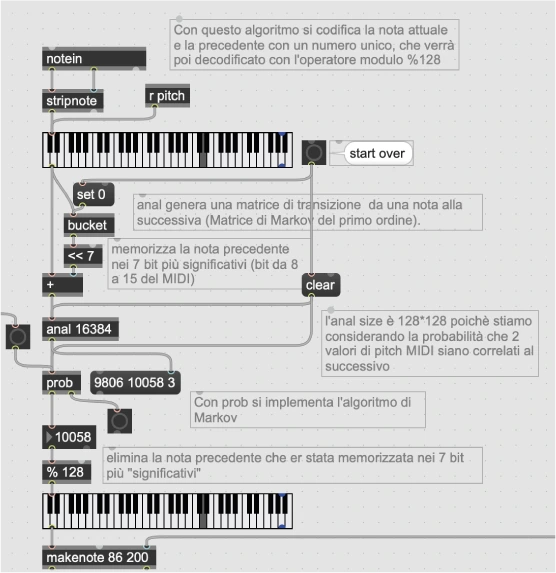
fig. 60
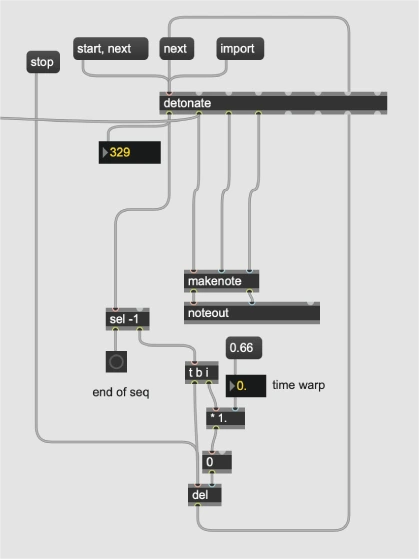
fig. 61
Algoritmo di caricamento di Midi File
L’oggetto prob, per ogni bang successivo genera un nuovo valore tra quelli
possibili dalla matrice di transizione.
Possiamo controllare la densità di attacco a attraverso una scelta pesata
casuale. .
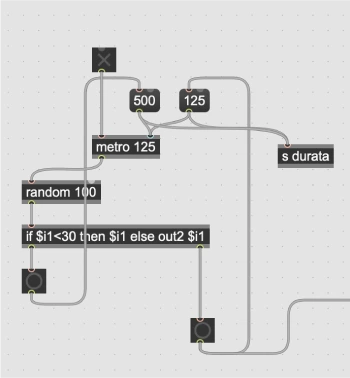
fig. 62
Oppure costruendo una una matrice di transizione per le durate..
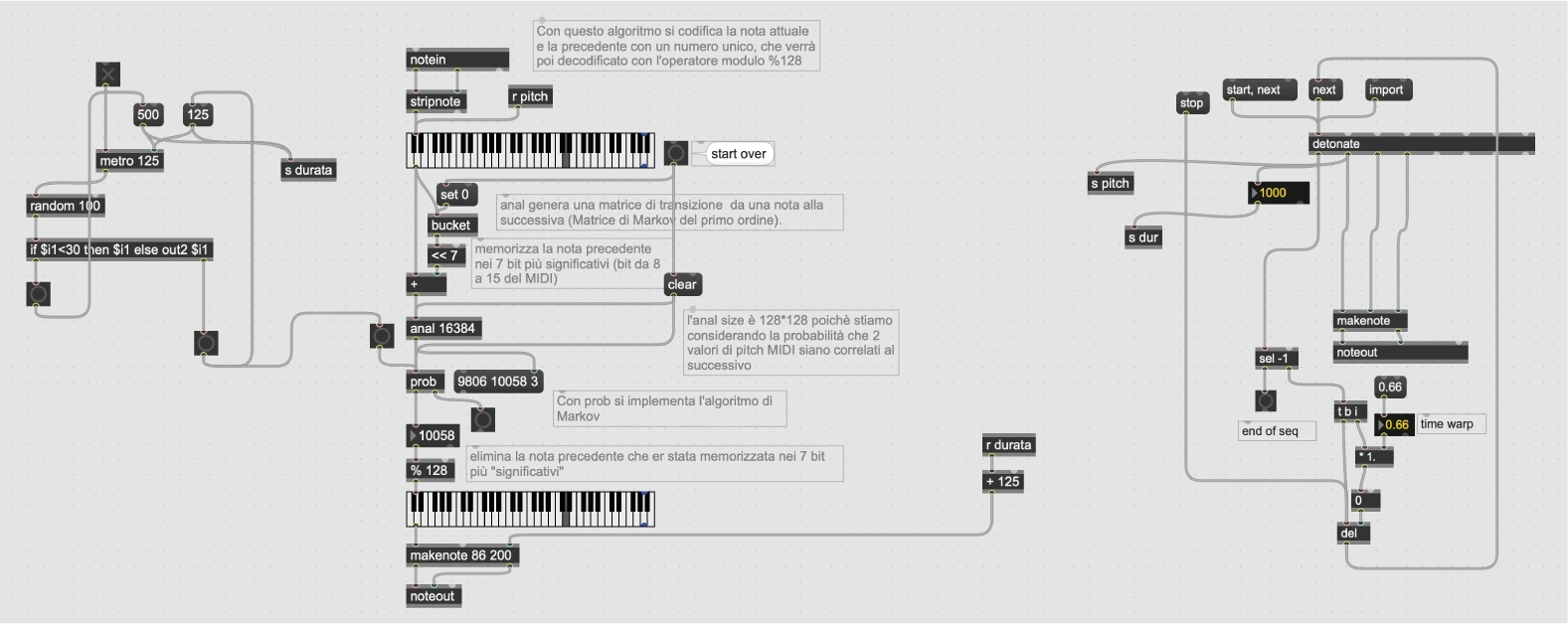
fig. 63