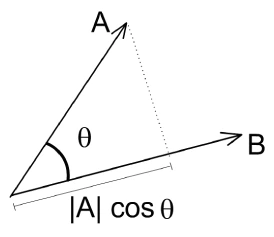
fig. 1
Il prodotto scalare nel piano euclideo è definito come il prodotto tra
le lunghezze dei due vettori per il coseno dell’angolo tra loro
compreso. Il suo risultato è un numero reale.
Il coseno può essere pensato come la proiezione (l’ombra) che un
vettore proietta sull’altro e può variare dal valore 1 (vettori
coincidenti) a 0 (vettori ortogonali) a -1 (vettori coincidenti con verso
opposto).
In altre parole si può pensare il prodotto scalare come una sOma di
quanto contribuisce il vettore A sul vettore B.

fig. 1
Il prodotto scalare si può estendere per vettori n-dimensionali ognuno con k componenti e in questo caso viene
definito come sommatoria dei prodotti delle rispettive componenti dei due vettori. Detti a e b due vettori
n-dimensionali.
$$a \cdot b = a_1 b_1 + a_2 b_2 + ... + a_n b_n = \displaystyle\sum_{i=1}^{n} a_i b_i$$
Ad esempio dato il vettore nello spazio tridimensionale \(a = [ 1, 2, -1]\) e \(b = [-1, 0,3 ]\) il loro prodotto scalare è
\([1,2,-1] \cdot [-1,0,3] = 1 \cdot (-1) + 2 \cdot 0 + (-1) \cdot 3 = -1 - 3 = -4\)
Altro esempio: \(a = [ 1, 2, -1]\) e \(b= [-1, 0, -1] = -1 + 1 = 0\) (vettori ortogonali)
Il prodotto scalare (detto anche prodotto interno) tra due vettori si
indica con i simboli ⟨⟩ detti Bra e ket con i due vettori separati da una virgola: \(⟨a, b⟩\)
Nell’esempio precedente \(⟨a, b⟩ = \displaystyle\sum_{i=1}^{n} a_i \cdot b_i\)